There are a lot (sometimes even heated) debates on the internet if there are 1000 or 1024 bytes in a kilobyte. This post is about why the correct answer is 1000 and how we ended up with this mess.

The prefix “kilo” is derived from the ancient Greek word χίλιοι (chilioi – pronunciation) and translates to “thousand”.

χίλιοι and its descendants χίλια (“modern” Greek for “one thousand”), and chiliad (“a group of 1000 things”) meant “thousand” for literally thousands of years and in its modern form as a prefix “kilo-” at least since 1795 when the kilogram was originally defined. This right there should theoretically end all discussions, but sadly that’s not the situation we are in 🤣.

🔗What happened?

Long story short: Computers.

Computers are designed around the binary system. That’s not a necessity but it’s technically one of the simplest options, because everything just boils down to two states, zero and one (oversimplified, but good enough for now). Consequently, a lot of sizes, dimensions, and amounts regarding computers end up having many twos as prime factors. This has to do with addressing, how hardware is scaled up and similar things, but that’s something for another time. This is also the reason why memory (for example RAM) always comes in sizes like 2, 4, 8 or 16 and not 11. This does not mean that everything that has to do with computers has to be an exact power of two, but there is a (again for technical reasons) tendency that a lot of powers of two are involved.

Let’s for example take the display resolution of the Nokia E60: 352 × 416. In total that’s 146’432 pixels. To see how many factors of two there are, we do a prime factorization:

$$ 146’432 = 2^{10}\cdot11\cdot13 $$ $$ = 2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot11\cdot13 $$

The factors don’t solely consist of twos, but ten are certainly lot of them.

To communicate this number to other people it would be quite a mouth full to always write 146432. To simplify it a bit we could use the well-established kilo- prefix and write it like so: 146.432k. Ok now that didn’t really simplify anything but we don’t need that amount of accuracy so we can round it to 146k.

But why did we get a fractional part in the first place? It’s because we divided by $1000$ with its prime factors $2^3\cdot5^3$ and because the original integer doesn’t have any factors of five, we end up with a fractional part.

So, what can we do about it?

Because we know that computer related numbers might have a lot of factors of two in them, we could divide by something that has only factors of two. Let’s look at the powers of two for some candidates: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024. WOW! Through a sheer mathematical coincidence(!) there is a number only built from twos that’s very close to 1000, which people using the metric system are so used to already. Lucky us!

🔗The slightly bigger kilo

People in the industry took immediate advantage of this (un)lucky coincidence and started to misuse the kilo – which again meant “thousand” for thousands of years – to sometimes mean 1024. This “slightly bigger kilo” was a dirty hack that was introduced, just because it felt convenient.

What made it more confusing still was that back in the day many computers only supported uppercase letters, so “K” was sometimes used to mean the correct kilo size of 1000 and sometimes 1024. With lowercase letters (for example in handwriting or on typewriters) one could distinguish between the correct kilo “k” meaning 1000 and “K” meaning 1024, but only in writing because “k bytes” is pronounced “kilobytes” and “K bytes” is also pronounced “kilobytes”. Over time even the distinction between “kB” and “KB” got more and more blurry and both could mean $2^{10}$ or $10^3$. What a mess.

In 1968 some people cared enough about it and proposed a few alternatives. None of those proposals caught on and everybody just continued doing what they wanted.

Computers were new and exciting, the industry was booming with excitement and investment, so none of the major players really cared to fix this problem because they had better things to do. In practice it was mostly fine, because companies and people that misused the SI “kilo-” as a binary prefix just added “K=1024” to the documents that used the “slightly bigger kilo” and called it a day.

🔗640K weren’t enough

Once the numbers started to grow – more memory, more storage, more speed, more everything – a limit was reached where “K” wasn’t enough to cut it and some people started to misuse the (since 1873) well established metric prefix mega- 1000² (M) when they referred to 1024² bytes. After the first storage devices reached the gigabytes, the situation was finally 𝕗𝐮ɕ𝓀𝐄∂.

In addition, the conversions were sometimes not even self-consistent and applied completely arbitrary. The 3½-inch floppy disk for example, which was marketed as “1.44 MB”, was actually not 1.44 MB and also not 1.44 MiB. The size of the double-sided, high-density 3½-inch floppy was 512 bytes per sector, 18 sectors per track, 160 tracks, that’s 512×18×16 = 1’474’560 bytes. To get to “1.44” you must first divide 1’474’560 by 1024 (“bEcAuSE BiNaRY obviously”) to get 1440 and then divide by 1000 for perfect inconsistency, because dividing by 1024 again would get you an ugly number and we definitely don’t want that. We finally end up with “1.44”. Now let’s add “MB” because why the heck not. We already abused those units so much it’s not like they still mean anything and it’s “close enough” anyways. By the way, that “close enough” excuse never worked when I was in school but what would I know compared to the computer “scientists” back then.

“1 MB” could now mean 1’000’000 bytes, 1’048’576 bytes, 1’024’000 bytes depending on the exact context, the phase of the moon, your monitors refresh rate and the taste preferences of the invisible unicorn that resides in your refrigerator.

This entire “KB” dumpster fire and the imperial system show very clearly that Americans can’t be trusted with choosing sensible units 😉.

🔗The Solution.

It was obvious right from the start and practically everybody knew it. Distinct binary prefixes that don’t redefine established SI prefixes. The only problem was that for some time there was no consensus on what symbols and names to use, but that changed when the binary prefixes were standardized in IEC 60027-2 in 1999. They are now incorporated into many standards and recommendations (IEC 80000-13, ISO 80000-1, SI, NIST) and are here to stay.

Today the only correct conversions are to either use SI prefixes (like 1 MB = 1000² bytes) or binary prefixes (1 MiB = 1024² bytes).

Using the names of SI prefixes but doing the conversion with 1024 is wrong. In fact, it always was wrong right from the start. It’s not like some people claim that it was correct until it was redefined in 1999. The kilobyte = 1024 byte idea always was unscientific and wrong and the IEC just standardized names for binary prefixes so people stop misusing SI prefixes for that. Even if a lot of people in the industry did (and some still do) misuse the kilo that doesn’t make it somehow correct.

🔗I don’t want to use gibibyte!

Even though some people say those binary prefixes “sound funny” – I guess that’s mainly because they are not used to them. And even if it would somehow be objectively true that they “sound funny” it would not be an argument for using SI prefixes in a wrong way. “Quark” also sounds funny, and we don’t have physicists wrongly calling them “electrons” just because they don’t like how the word “quark” sounds and the mass is “close enough”. If you really dislike the names of the binary prefixes, propose better ones but again: Misusing the names of SI prefixes is wrong.

If you don’t work in the industry just do whatever you want, seriously. You probably use speed and velocity interchangeably all the time without even thinking that velocity is a vector and speed just a scalar that describes the magnitude of that vector. You probably mix energy and power willy-nilly, but energy is the capacity to do work and power is the rate at which work is done. Journalists call all kinds of stuff “quantum leaps”, that have nothing to do with quantum mechanics. Lots of people don’t know that mass and weight are different things, and that mass is a scalar quantity intrinsic to an object and weight is vector that describes the force that is exerted on said object in a gravitational field because of its mass.

Even if you knew all that it’s very likely you sometimes (even intentionally) use the wrong expressions to keep the language simple. Nobody that says that “their phone died” means that literally. Using binary prefixes is not about being pedantic in everyday language, it’s about being precise in writing and formal settings. If a sysadmin colloquially says something about 128 “gig” or “gigabytes” of RAM, they are probably fully aware that it’s ackchyually 128 “gibibytes”.

In many situations it doesn’t even have any advantages to use binary prefixes. For example, in hard drives. One of my mine reports a total size of 16’000’900’392’960 bytes (the entire disk not the partition). That’s 16 TB. As with the Nokia example earlier I rounded because typically we are only interested in a few significant figures. The exact value with SI prefix would be 16.000’900’392’960 TB, and just for comparison with binary prefix the exact value would be 14.552’734’130’993’485’450’744’628’906’250 TiB. The original idea to use binary prefixes was to describe large numbers that are exact powers of two so we don’t end up with a fractional part that would force us to round. But that doesn’t really work out here and in a lot of other cases. Drive sizes are not bound to any powers of two and are completely arbitrary. So, in cases where you would have to round anyway there isn’t actually a benefit to use binary prefixes and because of that the size of the drive is typically labeled as “16 TB”. If you really want to use the 1024 conversion, even though there is no good reason to do so, it’s about 14.6 TiB (“Tebibyte”). This is also true for SSDs and other storage devices. Parts of their internal structure might be “binary based memory” but because of wear leveling and other internal details it practically never is a power of two.

Situations where you really should use established binary prefixes are when it’s about memory like RAM, CPU caches, buffer sizes, etc. If you are on Windows, you can check the amount of physical memory (RAM) you have like this:

> wmic memorychip get capacity
Capacity
17179869184
17179869184
17179869184
17179869184

Here is the prime factorization for the capacity of a single memory module:

$$ 17’179’869’184 = 2^{34} $$

RAM modules are always exact powers of two, so they are great candidates for binary prefixes. In this situation a single memory module has exactly 16 GiB and all four sum up to a total of exactly 64 GiB. It wouldn’t really make sense to use the conversion factor 1000 here and denote the memory modules as 17.2 GB. It would introduce useless rounding errors, and nobody would recognize 17.2 GB as a valid memory module size. So, when it’s about memory you should definitely use binary prefixes especially in written form. The extra “i” in “16 GiB” is not that hard to do and has the amazing benefit of not being wrong.

🔗Black sheep

Theoretically the situation should be solved by now and in theory there shouldn’t be a difference between theory and practice but in practice there is.

Remember, just because there are people (and even big corporations) using the wrong names for binary prefixes doesn’t automatically mean you should too. Just because there are a lot of people calling the “#” sign “hashtag” doesn’t mean you should too, because it’s wrong. The # sign is called (amongst other things) hash and if you combine it with a word to tag something (like #smartass) the entire thing is called a “hashtag”. If something gets used wrongly a lot (like hashtag) over generations, let’s say 100 years, it might really become a word for the “#” sign. A prominent example for that would be the word “nice” which originally meant “simple”, “foolish”, “ignorant”, “not knowing” but it’s meaning shifted. We are not yet at this point with binary prefixes and the wrong use of the word hashtag, there is still enough time to fix the problem before it’s broken for good.

🔗RAM modules, memory, caches

RAM modules are still typically labeled with “GB” instead of “GiB” by most vendors. I’m not exactly sure why because I guess it would not really confuse a lot of people to just add that “i”. Contrary to what a lot of people claim, the JEDEC Standard actually says the following about misusing SI prefix: “this practice frequently leads to confusion and is deprecated” but the standard probably needs more teeth and actually forbid misuse of SI prefix names instead of just calling them deprecated and enforce IEC prefixes.

A bit better is the situation with Intel. They seem to pretty consistently use the correct prefixes and only use “MB” when they mean the SI prefix and use “MiB” as a binary prefix. But they still mess up here and there and could be a bit more careful. This document lists “KiB” in terminology on 1.2 with the description “Kibibyte (1024 bytes)” which is fine, but the line before “KB” as “Kilobyte”. There is no “KB” with uppercase “K”. The unit for a kilobyte (1000 byte) is “kB”. In this document on the second page, they write “<4 kiB” but there is no unit “kiB”. The correct unit for kibibyte is “KiB” with an uppercase “K”. The simplest way to memorize that is probably to remember that all(!) SI and IEC prefixes start uppercase, except the SI kilo, which starts with a lowercase “k”.

AMD seems to be way sloppier with their units. Almost their entire website uses the wrong units, but in some documents, there are hints that some people at AMD know what they are doing. For example, this document uses the wrong memory prefixes throughout the entire document, but on the last page in the footnote fine print they use the correct units. In this document on page 3 the L1 cache with “512 KB” is wrong and should be “512 KiB”, the L2 cache right next to it with “8 MiB” is correct and the memory on the next line with “256GB” is wrong again and should be “256 GiB”, but to be fair the document doesn’t look too polished. Maybe the work of an intern? The Mac OS X and Microsoft Word metadata are still in the PDF if it wasn’t obvious enough because of Words default fonts. And finally, this document which again uses all the wrong units in the document itself but uses the correct units in the footnotes. Seems to be a pattern with AMD 🤣.

NVIDIA is also not as careful as Intel and mostly uses the wrong unit names, but not always. There are some cases where they use the correct units but as with AMD there doesn’t seem to be a consistent pattern. In this Holoscan SDK User Guide they use GiB and MiB but most of their consumer facing website uses GB to label GPU memory.

🔗Microsoft Windows

Microsoft is probably one of the biggest offenders, if not the biggest. Their operating system Windows has the biggest market share on consumer desktops and laptops and uses the wrong units. Remember the the 16 TB HDD from above? Here is what the properties tab of that drive looks like in Windows.

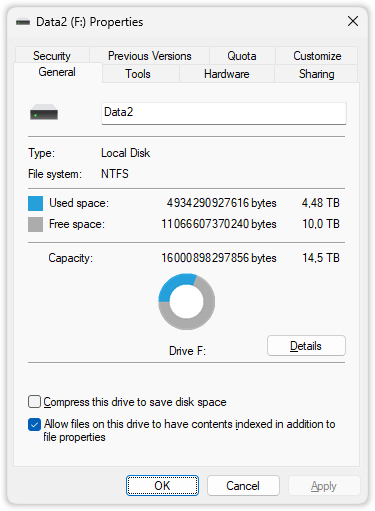
The capacity is about 2 MiB smaller than the number mentioned before, which is fine. That’s because this is the capacity of the partition and not the entire disk.

The problem is that Windows calculates TiB (with 1024) and then uses the wrong unit (“TB”) to label the result. For users that are unaware of this issue it looks like they paid for 16 TB and because of Windows think that they only got “14.5 TB”. At this point a lot of people blame the manufacturer of the drive, but Microsoft is the only one at fault here and should get their act together.

The other big players in the OS market Linux and Mac OS follow current standards and practices. Mac OS and most Linux Distros use SI prefixes and would correctly show that drive with 16 TB capacity. The Linux kernel itself is a bit different and mainly uses IEC prefixes and would show the drive as “14.6 TiB” which is also fine.

🔗Stop blaming drive manufacturers

The hard drive manufacturers are the big exception; they are among the few that consistently use the correct units. Not only that but using the SI units is the most sensible option here because hard drive sizes are arbitrary and practically never exact powers of two. Using the SI units will result in “bigger numbers”, and it might even be the case that hard drive manufacturers chose the SI units for this very reason, but that doesn’t change the fact that this is also objectively the most sensible option. We can also see in other sectors of the industry that it’s not only about “bigger numbers”. You could label a 16 GiB RAM module as 17.2 GB and it would be correct, but nobody does it because it doesn’t really make sense to do so, even if the number would be bigger 😅.

🔗(Un)lucky coincidence

Defining a kilobyte as 1024 bytes is – once you really think about it – intellectually completely dishonest. To show what I mean let’s go back in time to the 1940s when the first “modern” computers were developed and let’s pretend that ternary computers were more popular for various reasons (doesn’t really matter to make the point) and assume that the entire field moved in the direction of ternary computing.

Everything would be working with base three.

Instead of bits, we would’ve had ternary digits called trits, and instead of just zero and one, we would’ve had three states, probably (-1, 0, 1) or (0, 1, 2) — it doesn’t really matter. Rather than eight bits per byte, we’d probably have ended up with six trits per tryte. For the same reasons that our binary computers have memory with exact power of two sizes, in the alternative timeline we would have memory that is always exact powers of three. With growing numbers there would be an increasing need for a concise notation for large numbers, and because we don’t want to introduce rounding issues, we need to look at the powers of three for suitable values for prefixes: 1, 3, 9, 27, 81, 243, 729, 2187, …

Hey cool 729 seems pretty close to 1000. Let’s use that and just call it kilotryte. One kilotryte is exactly 729 trytes. Of course not. Nobody in their right mind would even for a second think that this would be a bright idea. But that’s exactly what we did in base two. Where would you draw the arbitrary line of it being “close enough” to a thousand to call it kilotryte? Would you consider 851 to be close enough to call it a kilotryte? Maybe 923? 974? I think part of why this happened was because our brain is a pattern matching machine and 1024 just looks quite a lot like 1000. It starts with the same two digits an ends with “24” which is exactly two dozen and a highly composite number. HCNs resonate with our brains because the come up a lot in our everyday lives like for example 12, 24, 60, 180, 360, etc.

I’m not sure this “kilobyte” accident would’ve happened if $2^{10}$ would land below 1000, let’s say 976.

Two was actually the most unluckiest base possible to lure us into calling it a kilo. Here is an interactive number line to explore how close/far the other bases land to 1000. The values are scaled logarithmically. After two, the next “best” bases would be 31 and 33 (excluding 4 and 32 because they are powers of two and also land at 1024) which would land at 961 and 1089 respectively.

No matter how close – even at 999 – if it’s not exactly one thousand it’s just sloppy to call it a kilo and for this reason it is and always was wrong to call 1024 bytes a kilobyte. This “close enough” mindset is probably fine for computer hobbyists but it’s definitely not computer “science”. In science you must be careful and precise with your words and definitions and especially your units. Trying to redefine the kilo was the exact opposite. It was careless and not well thought trough.

Trying to redefine what a kilo means for a specific purpose is a bit like the situation with the Indiana Pi Bill (Video by Numberphile) where somebody wanted to redefine π to 3.2 by law 🤣. The world (at least Indiana ^^) can call themselves lucky that a mathematician noticed that stupid idea. If it would’ve been a “computer scientist” they would’ve probably said that it’s close enough and totally fine to also use π for 3.2. Not a problem. Just make it dependent on the context. If you need π in a computer related context it means 3.2 and in all other contexts it means 3.1415926… 🤦.

🔗Recommendations

Here are a few things you should keep in mind when thinking about what units to use:

1. Always use the correct prefixes (especially in writing).
2. Only use binary prefixes for numbers that are exact powers of two.
   For example, for memory, cache and buffer sizes, etc. Only when there is a very good technical reason should you really use them. Do not use them for storage and file sizes.
3. Use SI prefixes for everything else.
   Like for capacity in storage devices, CDs, DVDs, file sizes, partition sizes. Only use binary prefixes if you want to communicate that a given amount is exactly(!) that size. For example, if you document some kind of index file that is always is exactly 8192 bytes long use “8 KiB” but if you are listing arbitrary file sizes (for example word documents) use “kB” and “MB” because they are arbitrary and have nothing to do with powers of two. The quantity should be intrinsically related to binary to use binary prefixes. Just because a distance is coincidentally 1024 meters you shouldn’t convert it to “1 kibimeter”, there is nothing intrinsically binary about distances.
4. Be aware that others might use it wrong.
   Even though many already use the correct prefixes and units there are still people and companies out there that either don’t know or do know and either don’t care or have some form of excuse to use the wrong units.

🔗Valid and invalid units

With binary prefixes, SI prefixes and units for bits and bytes there are a lot of possible combinations. Be careful when using them especially with capitalization. remember the the first letter of all prefixes is uppercase with only one exception, the SI “kilo-” prefix with the lowercase letter “k”. The unit for a bit is “b” (lowercase because a bit is a small unit of information) and for a byte is “B” (uppercase because a byte is a larger unit of information).

Here are some units that are either wrong or probably not what you meant:

• KB: That’s the most widespread wrong unit. It was historically used to sometimes mean 1000 bytes and sometimes 1024 bytes. Please do not use that. “K” is neither a SI prefix nor a binary IEC prefix. “K” is the temperature unit Kelvin. The unit for 1000 bytes is “kB”, for 1024 bytes is “KiB”, for 1000 bits is “kb” and for 1024 bits is “Kib”.
• kiB: All the binary prefixes start with uppercase, even the “kilo binary”. The correct unit would be “KiB”
• mb: That’s theoretically a correct unit but it means “milli-bit” and probably not what you meant. To denote a megabyte (a million bytes) the correct unit would be “MB” and a megabit (a million bits) would be “Mb”. Megabits are typically used in network speeds like in “8 Mb/s”.
• MIB: Only use that if you mean the Men in Black. If you mean 1024² bytes you should use the correct unit “MiB”.

🔗Footnotes

🔗How and why I cherry picked the “Nokia E60”

Some might have wondered, why I used the Nokia E60 in the example with the prime factorization and how I picked it. After deciding that I wanted to go with screen resolutions, I started with Wikipedia’s list of common resolutions. I wanted my example to have a few properties to show the situation more clearly.

1. Neither width nor height should be exact powers of two.
   The example should show that it’s not a requirement for those numbers to be exact powers of two and it should not be obvious just from looking at the numbers that they contain a lot of factors of two. For example, the screen resolutions 1024 × 1024 and 1024 × 768 contain well recognized powers of two and would introduce the number 1024 as a “computer thing” earlier than I wanted.
2. The sides should not contain any factors of five.
   It should not be possible to simplify the result after dividing by 1000 at all. For example, the classical VGA resolution 640 × 480 would result in 307’200 total pixels and has two fives in its prime factors. After dividing by 1000, one would get 307.200k and even if we end up with a fractional part it could be simplified at least a little bit by dropping the trailing zeros to get 307.2k. So, with excluding resolutions containing a factor of five I ensured that we won’t end up with trailing zeros that could be simplified.
3. The resolution should not be in the “megapixel” range.
   I wanted to introduce the prefixes one by one, so it was a requirement for the first example to be in the “kilopixel” range and also not be in the high kilopixel range. Resolutions like 1152 × 768 (=884’736 pixels) and 1152 × 864 (=995’328 pixels) would be in a high enough range to just be rounded up to “1 megapixel” in practice.
4. The result should be divisible by 1024.
   To make the benefits of dividing by 1024 more obvious the result should not have a fractional part after dividing by 1024. Because I limited myself to the kilopixel range sometimes a lot of factors of two are still not enough. For example, the resolution 368 × 480 (=176’640) has nine factors of two but to be divisible by 1024 we need at least ten.
5. The example should be known, at least a little bit.
   The resolution 384 × 224 for example would be a good candidate according to the criteria listed before, but the “Capcom CP System (CPS, CPS2, CPS3) arcade system boards” is probably not as well-known as some classic Nokia phone from 2005.

🔗Obligatory xkcd

🔗Links

• https://en.wikipedia.org/wiki/Timeline_of_binary_prefixes
• https://physics.nist.gov/cuu/Units/binary.html
• https://mathworld.wolfram.com/Kilobyte.html