If someone sent you a link to this page, then you probably already have an answer to the question. If you don’t or your problem used different numbers, I want you to take a minute and solve the following problem:
$$ \Large 6÷2(1+2) = $$
Got it?
If you are sure the answer is one, I’m sorry I must break it to you, but you are wrong. You are sure that the answer is nine? Congratulations ‒ you are also wrong.
(If you got something besides 1 or 9 you made a mistake, double check it before you continue reading.)
But how can everybody be wrong?
Because it’s not a math problem! It’s a communication problem because it’s (intentionally!) written in an ambiguous way.
Strong feelings?

There are quite a few people who are certain(!) that their result is the only correct answer and even develop very strong feelings about that. If you are one of them, ask yourself: What kind of evidence/information would it take to convince you, that you are wrong. Really think about it. Is there anything somebody can tell you or show you, that would change your mind about it. What, if anything, would convince you?
If there is nothing that would change your mind, then I’m sorry I can’t do anything for you. Seems like you’ve already made up your mind and there is no point in reading the rest of article. If you are not willing to accept the possibility that you are wrong about this (or anything really) then you stopped learning ‒ at least about things that contradict your current beliefs. If you are so sure that you are right and already “know it all”, why bother and even read this? There is no comment section to argue. Just leave and do something else 👋.
If you are however willing to accept the possibility that you are wrong, if I show you some convincing stuff, this article might be for you.
How can math be ambiguous?
In short, the issue with practically all those “viral/tricky” math problems boil down to operator priority with “implied multiplication by juxtaposition”. Implied multiplication by juxtaposition (or just implied multiplication) describes a situation where two expressions, like in our example $2$ and $(1+2)$ are joined without any (visible) operator like so: $2(1+2)$. This is a valid notation for a multiplication but the order of operations it’s not well defined with respect to regular explicit multiplication. There is no single clear norm or convention.
The reason why so many people disagree is that there are two widespread, but conflicting conventions about the order of operations for implied multiplication by juxtaposition.
-
Weak juxtaposition
Implied multiplication by juxtaposition has the same(!) priority as explicit (normal) multiplication (and division) -
Strong juxtaposition
Implied multiplication by juxtaposition has higher(!) priority than explicit (normal) multiplication (and division)
If you think one of those two conventions is wrong or not a valid convention (especially if you have strong feelings about it) I want you to remember the Strong feelings? section and try to delay your judgment.
It’s now easy to construct “viral math problems” by writing a single-line expression (without a fraction) with a division first and an implied multiplication after that. Here are some examples I found online:
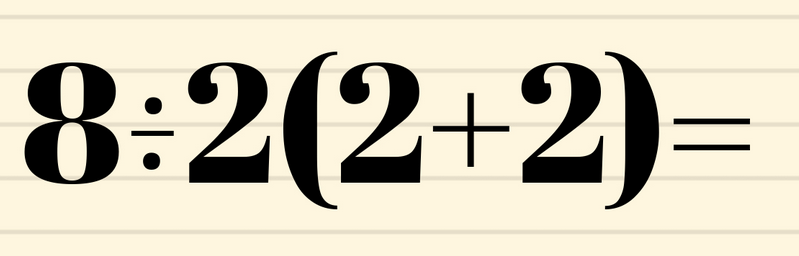

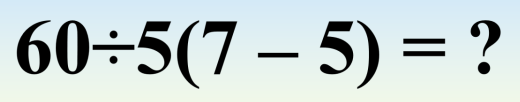


Note how none of them use a regular multiplication sign, but implicit multiplication to trigger the ambiguity.
How to solve it?
Because the notation is ambiguous without more context you first must find out what convention to use. The best way to do that, would be to ask the original author what they meant or if that’s not possible try to deduce what convention to use based on the context. If it’s a school test, ask you teacher – maybe they can write it as a fraction to make it clear what they meant. If your teacher doesn’t give a straight answer or doesn’t understand your question you should probably stick to the weak juxtaposition convention. If you are a student at university, a scientist, engineer, or mathematician you should really try to ask the original author what they meant because strong juxtaposition is pretty common in academic circles, especially if variables are involved like in $a/bc$ instead of numbers.
Once you know what convention to use to interpret the original question, you should start by rewriting the original expression $6÷2(1+2)$ as a fraction. Interpreted with weak juxtaposition the problem looks like this (because division and implied multiplication have the same precedence, so we solve from left to right):
$$ \frac{6}{2}(1+2) = 9$$
Now let’s interpret the question with strong juxtaposition. Because implied multiplications have a higher priority than divisions with this convention it looks like this:
$$ \frac{6}{2(1+2)} = 1$$
So, the original problem is not a math problem, the math is actually trivial. The problem is that those expressions are intentionally written in an ambiguous way without telling you what they meant or which convention to follow to stir up drama.

This ambiguity is only there because of the implicit multiplication. If there would be an explicit multiplication, there would be no ambiguity because explicit multiplication and division have the same order in both the strong and(!) weak juxtaposition convention and thus would lead to the same answer.
$$ 6÷2\times(1+2) = 9 $$
(If you still think that the answer is one, even when using explicit multiplications you made a different mistake, I’ll address that later. You can try to enter the expression with explicit multiplication into any credible calculator and the answer will always be nine.)
But my calculator says …
Calculators are actually one of the reasons why this problem even exists in the first place. Because so many devices like calculators, computers, typewriters, and smartphones let you write “line-based” text, it led to the development of various in-line notations.
As we saw before with proper structured math notation and using fractions for division it’s clear what order of operation was intended. But most (especially not very modern) consumer calculators and practically all online calculators only have a single line input field, so you are forced to use in-line notation. With most in-line notations there are some situations with conflicting conventions where you must be careful. On any single calculator model the notation is not! ambiguous, because the manufacturer decided what convention they want to follow, and they stick to that. If they did a good job, they even documented the conventions they chose in the manual of the calculator.
Because there is no clear standard about the priority of implied multiplications, different manufacturers use different conventions. More often than not even the same manufacturer uses different conventions for different calculator models/series depending on their intended use-cases.
Casio fx-991MS vs fx-991ES
To make it really clear how there is no agreed upon (single) standard for implied multiplication here is a comparison of two very similar calculators I personally own.

Now let’s take a quick look into the manuals of those two calculators.

| Calculator | Manual |
|---|---|
| fx-991MS | https://support.casio.com/pdf/004/fx115MS_991MS_E.pdf |
| fx-991ES | https://support.casio.com/pdf/004/fx-115ES_991ES_Eng.pdf |
As you can see the fx-991MS implements the implicit multiplication with a higher priority than a regular multiplication (strong juxtaposition). They deliberately split the category in two, making a distinction between implicit multiplication with variables and other forms of implicit multiplications.
The fx-991ES on the other hand uses the same priority for implicit multiplication and explicit multiplication (weak juxtaposition).
This example shows that order of operations in practice is not as simple as one might initially think. Two very similar calculator models from the same manufacturer handle those cases differently and none of those two calculators is “wrong”, they just follow different conventions. It’s also clearly not a bug as some people suggest. Bugs are – by definition – unintended behavior. That is not the case here. The behavior is intended and even carefully documented in the manual. It was a deliberate choice Casio made here. It’s also not cherry picked, Casio has multiple calculators that use strong juxtaposition and multiple calculators that use weak juxtaposition.
It also doesn’t depend on the age of the calculator, but what the intended use-cases are.
Relatively recent (2023) calculators from the Casio ClassWiz (CW) Series like the fx-991CW and fx-85GTCW use strong juxtaposition for example, but not because they are new and the weak juxtaposition is only used by old calculators, but because they are scientific calculators. There is typically a tendency for calculators which are intended for scientific purposes to use strong juxtaposition and for calculators intended for basic, educational and light scientific use-cases to follow weak juxtaposition.
And again: With explicit multiplication there is no confusion:

Maybe Casio is weird?
Could be, if it were only Casio that seemingly couldn’t pick just one of those two conventions and stick to it. But it’s not only them. TI (Texas Instruments) also has some calculators that use strong juxtaposition and some products that use weak juxtaposition.
“Implied multiplication has a higher priority than explicit multiplication to allow users to enter expressions, in the same manner as they would be written. For example, the TI-80, TI-81, TI-82, and TI-85 evaluate 1/2X as 1/(2X), while other products may evaluate the same expression as 1/2X from left to right. Without this feature, it would be necessary to group 2X in parentheses, something that is typically not done when writing the expression on paper.
This order of precedence was changed for the TI-83 family, TI-84 Plus family, TI-89 family, TI-92 Plus, Voyage™ 200 and the TI-Nspire™ Family. Implied and explicit multiplication is given the same priority.”
Maybe TI and Casio are both in on the conspiracy? If so, here is a screenshot from the HP (Hewlett-Packard) 30S manual:
So, the HP 30S follows the strong juxtaposition convention and the HP 9g follows the weak juxtaposition convention.
Canon for example has the F-715SG which uses the strong juxtaposition and the F-730SX which uses the weak juxtaposition convention.
Sharp is a bit of an exception here, because all their other scientific calculators seem to use the strong juxtaposition convention. Maybe they have a very strong opinion on that, or they use the same calculation engine for all their calculators.
Google uses the same priority for explicit and implicit multiplication.
Desmos and GeoGebra try to force the user into using fractions (which is a good design decision if you ask me), so it’s not even trivial to write an ambiguous expression there, but with copy-paste we can try to trick them. Pasting $6÷2(1+2)$ into Desmos will yield $9$ (weak juxtaposition). GeoGebra simply won’t let you write it without a fraction, and they convert it to a fraction the moment you paste it in. Well done GeoGebra 👏.
A lot of other tools like programming languages, spreadsheets, etc. don’t allow implicit multiplication syntax at all.
The Best Solution (IMHO)
Some calculators like the android calculator HiperCalc let you choose if you want weak or strong juxtaposition. This gives you more control about how you like the calculator to behave in these situations.
Wolfram|Alpha only uses strong juxtaposition between named variables, but weak juxtaposition for everything else. This might seem strange and inconsistent at first but is probably the least surprising behavior for most people in most cases. Most importantly, they rewrite your input as a fraction and give you immediate feedback about how their engine is going to interpret your input.
| Expression | Result |
|---|---|
| 6/2(1+2) | 9 |
| 6/2x where x=3 | 9 |
| 6/xy where x=2, y=3 | 1 |
Wolfram also has some good advice on MathWorld.
“Special care is needed when interpreting the meaning of a solidus in in-line math because of the notational ambiguity in expressions such as $a/bc$. Whereas in many textbooks, $“a/bc”$ is intended to denote $a/(bc)$, taken literally or evaluated in a symbolic mathematics languages such as the Wolfram Language, it means $(a/b)×c$. For clarity, parentheses should therefore always be used when delineating compound denominators.”
— Weisstein, Eric W. “Solidus.” From MathWorld – A Wolfram Web Resource. https://mathworld.wolfram.com/Solidus.html
Another option would be to solve it like the Casio fx-9860 GII (never used it personally). The calculator automatically rewrites your input and places parentheses to make clear how it interpreted the input.
Chapter 2.1 “Multiplication Operations without a Multiplication Sign”
If you execute a calculation that includes both division and multiplication operations in which a multiplication sign has been omitted, parentheses will be inserted automatically as shown in the examples below.
This is a nice solution, but in long calculations it might not be obvious, that the calculator placed some parentheses off-screen. But to be fair the user should’ve written those parentheses in the first place.
What about PEMDAS?
ℹ️ First things first
Multiplication and division have the same priority, they are “mathematically speaking” the same operation. This also applies to addition and subtraction. One is just the inverse function of the other. There is no rule about “multiplication before division” or “division before multiplication” they always have the same priority.
Mnemonics like PEMDAS, BEDMAS, PEDMAS, BIDMAS, BODMAS, XMAS (jk), etc. are used by some schools and teachers in some countries to teach children the bare minimum(!) about order of operations in mathematics. In no way do any of the mnemonics represent any standard or norm in mathematics. They are tools for educating children. In most cases it’s good enough, because most children don’t become mathematicians later in life and if they do, they will learn all the other important stuff about the order of operations later.
Educating children is hard. Children typically (depending on the country you live in) go to school for about ten years or even longer if they go to college or university. It’s such a long time, because it’s hard to pump so much knowledge into children and teenagers. But teaching so many different topics to children is only possible because most of it is simplified a lot. The classic Bohr model of the atom almost everybody is taught in school is a simplification – atoms don’t look like solar systems. Classical (Newtonian) mechanics: accurate for almost all practical use-cases, but fails for very small, very fast or very heavy objects. We try to give children a good overview about the world and try to teach them “how to learn”, so after school teenagers and young adults can learn new stuff themselves without necessarily relying on teachers guiding them all the way through.
Most people were also taught about the planets in our solar system and depending on how old you are, that there are eight or nine planets in our solar system. Maybe you’ve heard of the mnemonic (or a similar one) “My Very Educated Mother Just Served Us Nine Pizzas” to help you memorize the planets in order. Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto (not a planet, according to the IAU 2006 definition of “planet”).

As said earlier, mnemonics are tools to memorize stuff. The mnemonic about the planets and your “very educated mother” is not astronomy. It’s a tool to teach something to kids who are not astronomers. The same is true for “PEMDAS”. It’s a mnemonic to teach kids. It has nothing to do with mathematics really. Using “PEMDAS” to argue about the order of operations in mathematics, is like using the “pizza”-mnemonic to argue that Pluto is a planet (which it is not). Scientific knowledge (and conventions for that matter) are often simplified into mnemonics for students to help them memorize stuff, but those mnemonics don’t have any real power in the other direction. “Nine Pizzas” don’t dictate anything about Plutos planet-status, and “PEMDAS” doesn’t define the order of operations in mathematics.
Math notations and conventions evolve exactly like natural languages through the people who use it. A lot of it is heavily based on historical thanks and work from previous generations. Natural languages evolve through people that speak that language and mathematical notation is mostly shaped by scientists, mathematicians, and engineers, because they use math a lot in their daily lives. There is no definitive norm, standard or convention of notations and order of operations in the same way that there is no “the dictionary”. There are lot of different dictionaries and some words appear in almost all of them (like “multiplication before addition”) and some words only appear in half of them (like “implicit multiplication by juxtaposition”) and some words only appear in a hand full of dictionaries that are only used by a specific profession in some rare use-cases, and for all those words the definitions in the dictionary might even be slightly different. And exactly like natural language most parts, especially the foundations, are pretty solid and evolve very slowly, but there are also modern developments: For example, in natural language words like “selfie”, “emoji”, “vlog”, “podcast” are pretty new and in mathematics for example the up-arrow $\uparrow$ is pretty new (1976). It doesn’t mean that these words or notations were never used before or that the concepts they describe are new, but they were popularized recently and found widespread adoption.
You can also (but I wouldn’t recommend it) invent a completely new math notation from scratch the same way you could just invent a new language with all the rules you like. The only problem is (with your math notation and/or your invented language) that it’s not a very useful tool, if nobody besides you and your friends uses this language and/or notation. And exactly like in natural languages it’s not a simple process to change those conventions globally. So, no matter if you like weak or strong juxtaposition more, it doesn’t matter, we should avoid those ambiguous situations as long as there is no real global consensus (at least amongst experts) on that topic. Same with natural languages where we should try to avoid sentences like “I saw the man with the telescope”, because it’s not clear if you saw him through the telescope or saw him holding (or looking through) a telescope. It doesn’t matter what you think the more likely scenario is – if there is no real consensus you should avoid it if you want to be precise.
Because math notation has practically nothing to do with “truth” and everything to do with conventions, it should also be clear why there are no arguments or proofs for any side. It’s only a matter of taste and how widespread a convention or notation is. It’s a bit like the word “to overlook”. It can mean “to watch over or supervise” or “to fail to notice or perceive”. There are no arguments or proofs about what definition is correct. As long as the word is used in both situations you have to make sure that it’s clear from the context which definition you meant.
Wrong explanations

In the past and during the research for this article I found a lot of explanations online that were either half-assed or just plain wrong. I want to go through the most popular ones to debunk them and hopefully clear up some misconceptions – or to finally confuse everybody, let’s see.
“Multiplication before division”
As mentioned at the beginning of the “PEMDAS” section, multiplication (explicit) and division have the same precedence and are evaluated from left to right. You either were taught something wrong or you misremember it. IMHO the mnemonics would be better without “division” and “subtraction”, because it would force people to think about it before blindly applying something the wrong way – “PEMA” for example. Parentheses, exponentiation, multiplication, addition.
In Germany and Austria (not sure about Swiss) children are typically taught “Punkt vor Strich” which pretty literally translates to “Dot before line” to help them remember that multiplication ($\cdot$) and division ($:$) are evaluated before addition ($+$) and subtraction ($-$). I really like the approach, but maybe I’m biased because I’m from Austria. Even years after primary math classes people don’t just randomly get confused about multiplication and division and if they are the same priority or not. In “Punkt vor Strich” it’s perfectly clear that they are the same category. Regarding parenthesis and exponents students typically don’t learn the order of operations through some mnemonics they remember them through exercise. IMHO it’s a more natural approach to learn through practice instead of trying to remember some random acronyms.
Back to “multiplication before division”. This misunderstanding is also the reason why some people get $1$ even with explicit multiplication $6÷2\times(1+2)$, but that’s incorrect and nobody that does any amount of serious math would consider that a good or valid convention. Of course, you can say “that’s just my convention of doing things”, but that would be as ridiculous as calling forks “pointy-pokey” while everybody else still calls them “forks”. Even if you teacher in school taught you, they are called “pointy-pokey” you are wrong, nobody says that and nobody uses “multiplication before division” or “division before multiplication”, they have the same precedence.
All cases I saw, where somebody claimed they do multiplication first and then division, they only do so for implicit multiplication, so the actual rule they follow is just the strong juxtaposition convention. For example, the American Physical Society state in their Style and Notation Guide on page 21 that they do “multiplication before division”, but you must be careful to not take that out of context. On the same page in the section “Multiplication signs” they also state to “not use $\times$ to express a simple product” and “The center dot also should not be used to mean a simple product.”. So, they really do “multiplication before division” and at the same time practically (there are two exceptions) forbid explicit multiplications, so they also basically follow strong juxtaposition.

Nobody at the American Physical Society (at least I hope) would say that 6/2×3 equals one, because that’s just bonkers.
“The problem is the obelus (÷) division sign.”
Some people claim that the problem has something to do with the kind of division symbol used and that it makes a difference if one uses $÷$ (obelus), $:$ (colon) or $/$ (solidus), but that is not the case and they can be used interchangeably without any difference in meaning. There are no widespread conventions, that would attribute different meanings or priority to them.
Some people cite ISO 80000-2 for this, most of them probably because they read the Wikipedia article “Obelus” which references ISO 80000-2. I checked the most recent version to find out if there is any context that explains why it should be avoided. The only part where the obelus is mentioned in the document is in the section about division with the following quote:
“The symbol ÷ should not be used.”
— ISO 80000-2:2019, Section 10 “Operations”, 2-10.6
(Second Edition 2019-08, Corrected version 2021-11)
So, sadly no context in the document itself, why it should be avoided, but the other parts of the Obelus Wikipedia article are pretty informative too. The obelus can be confused with some other symbols like † (Dagger), ⁒ (Commercial minus sign) which was only added to the Unicode Standard in 2017 – up until that point ÷ was used to represent division and the commercial minus sign. It can also be confused with the + (Plus) sign or % (Percent) sign. So, it’s actually a good idea for a standard to forbid a sign that can be confused with so many other things when there are other (also well established) alternatives.
But if you read the ÷ symbol as a division sign (instead of confusing it as an addition, subtraction, or percent) there were never any conflicting conventions about the order of operations. So just use the division symbol you like the most, but keep in mind that the obelus could be confused with other symbols or operations, but in my experience most people today would interpret the obelus as a division sign and most of the social media comments I saw about this topic seem to agree. I can’t remember reading a comment where somebody suggested that ÷ is a “commercial minus sign” or a percent sign. The discussion was always about the order of operations and for that the division symbol does not matter.
$$ 6÷2\times(1+2) = 9 $$ $$ 6:2\times(1+2) = 9 $$ $$ 6/2\times(1+2) = 9 $$
The ambiguity only emerges when implicit multiplication is used!
In a lot of norms and standards the rules are stricter than they need to be, just in the name of clarity. For example, most standards forbid multiple divisions with inline notation, for example expressions like this $12/6/2$ are forbidden in most notable standards to prevent confusion, even if most experts and all calculators I can think of would tell you, that the answer is $1$ (and not $4$). To be standard conform you’d have to write $(12/6)/2$ to make the order even clearer and to prevent mistakes. This requirement is not in place because there is any ambiguity or real disagreement here, it’s just because of “better safe than sorry”.
“Historical Usage 1917”
In 1917 Nels Johann Lennes wrote a letter to “The American Mathematical Monthly” (Vol.24 No. 2) for the Questions and Discussion section “Discussions: Relating to the Order of Operations in Algebra” and tried to establish the rule:
“All multiplications are to be performed first and the divisions next.”
Funny enough all the examples that N.J. Lennes list in his letter use implicit multiplications and thus his rule could be replaced by the strong juxtaposition convention for all his examples and would make way more sense than “multiplication before division”. If one would follow his rule to the letter, the expression $ 6/2\times3 $ would be evaluated to $1$ which practically nobody especially scientists and mathematicians (not even in 1917) would think is a very bright idea, because “division and multiplication” had the same priority for a very long time, because one is just the inverse of the other.
“Some calculators are buggy.”

As stated in the paragraph about calculators, it can’t – by definition – be a bug. A bug is “unintended” or “unwanted” behavior and that’s clearly not the case here, when manufacturers like Casio, TI, HP, Canon, Sharp, all describe it in the manual with remarkable accuracy how the feature should (and does) work. Some claim it’s just a weird decision by a single company, but that’s also clearly not the case as we saw earlier.
“Something, something, distributive property, something ….”
The distributive property is just a property that applies to some operations, for example like multiplication.
$$ x\times(y+z)=x\times{}y+x\times{}z $$
It has nothing to do with the order of operations. I’ve no idea where this idea comes from because there aren’t any primary sources (at least I wasn’t able to find any), but there are a ton of comments about that on “viral math” social media posts. My guess is, that it has to do with “a feeling” some people without formal math training have, that somehow the factor has a stronger connection to the expression inside the parentheses and thus should be calculated (distributed) first. This “feeling” (again I’m guessing here) probably comes from a (maybe even unconscious?) preference for the strong juxtaposition convention. But without knowing that this is even a thing, they just reference the distributive property because that’s something they know.
So back with the original numbers: After calculating the stuff inside the parentheses we are left with $6÷2(3)$. If we follow the strong juxtaposition convention, we must multiply $2$ and $3$ first because they are juxtaposed together. It has nothing to do with the $3$ being inside parentheses. Those parentheses are only there, because just juxtaposing $2$ and $3$ together like we do with variables (like in $6÷xy\text{ where }x=2, y=3$) is not possible, because without parentheses it would result in $6÷23$ and that’s clearly not the same, because we already have a meaning for juxtaposing digits together to build bigger numbers in our decimal positional numeral system. So, the parentheses do not force the multiplication. The parentheses are only there to make it clear that we are implicitly multiplying two separate numbers.
What about the real world?
In contrast to some viral math problems on social media, where problems are intentionally written to drive engagement through disagreement, mathematicians and engineers don’t do that. They always try to be as clear as possible, use proper notation or throw in some parentheses to prevent ambiguity. Sometimes the context also helps to make things clearer.
Take for example an engineer that writes $r=C/2\pi$ on a back-of-the-envelope calculation to calculate the radius ($r$) of a circle based on its circumference ($C$). With the context that the engineer is trying to calculate the radius of a circle it’s clear that they meant $r=C/(2\pi)$ and not $r=(C/2)\pi$.
For important documentations and calculations there are norms and guidelines in place that tell people to be extra careful with ambiguous notation. Let’s see for example the relevant section of ISO 80000-1:2022 namely Section 7.1.3., here a quick excerpt:
When symbols for quantities are combined in a product of two or more quantities, this combination is indicated in one of the following ways: $$ ab, a\ b, a\cdot{}b, a × b $$ Division of one quantity by another is indicated in one of the following ways: $$ \frac{a}{b},\ a/b,\ ab^{-1},\ a\cdot{}b^{-1} $$ Writing $ab^{-1}$ with a space between $a$ and $b^{−1}$, as $a\ b^{-1}$, avoids misinterpretation as $(ab)^{−1}$.
and now to the important part relevant to our topic
These procedures can be extended to cases where the numerator or denominator or both are themselves products or quotients. In such a combination, a solidus (/) shall not be followed by a multiplication sign or a division sign on the same line unless parentheses are inserted to avoid any ambiguity.
The document then continues with some more examples to show in what situations parentheses are required (or not).
In software engineering most typical programming languages don’t allow omitting the multiplication operator, thus the order of operations is pretty clear when it comes to $+,-,*$ and $/$, but there are a lot more operators in programming languages where it is not as clear, so professional developers often split their calculations into multiple steps or make extensive use of parentheses to clearly communicate and document the intent.
Some programming languages even have static code analyzer rules you can tweak to remind you of using parentheses to make the order of operations as clear as it can be (e.g., “.NET IDE0048 – Add parentheses for clarity”).
Other ambiguous situations with juxtapositions
Let’s say we want to clean up and simplify the following statement … $$ o×s×c×(\alpha+\beta)$$ … by removing the explicit multiplication sign and order the factors alphabetically: $$ cos(\alpha+\beta) $$ 🤣 Nobody in their right mind would remove the explicit multiplication sign in this case and write the expression like that, because it would completely change the meaning of it. Nobody will interpret $cos(\alpha+\beta)$ as a multiplication of four factors. Implicit multiplications of variables with expressions in parentheses can easily be misinterpreted as functions because the notation of how we evaluate functions is the same.
So, ambiguity really hides everywhere. Here is a blog about a similar topic by NumWorks: An Improved Parser!. Personally, I’m not convinced of the design choice of basically trying to “autodetect random stuff” until something works because in a worst-case scenario the user has no idea how the calculator interpreted the input. IMHO it would be smarter to only allow the calculation if the input is unambiguous. If it’s not unambiguous force the user to write explicit multiplications or rewrite the input to make clear to the user how the calculator understood the input (like the Casio fx-9860 GII).
Even more ambiguous math notations
Implicit multiplication is far from the only ambiguous math notation and convention. Notations in math are used to communicate mathematical ideas and concepts in writing, and as every other communication tool it has its trade-offs. Of course, we could try to invent and force notation that is never ambiguous, but that would lead to a very convoluted mess that’s hard to read and write. We could force everybody to use some stack-like notations like RPN (Reverse Polish notation) or write brackets everywhere. It would be very tedious so it’s often preferable to use a notation that can in some cases be ambiguous if we are not careful and then try to navigate around those ambiguous situations by not writing/using them, or by providing context that makes it unambiguous.
Links about various potentially ambiguous math notations
- “Most ambiguous phrases and notations in maths” (math.stackexchange)
- “Absolute value notation is ambiguous” (math.stackexchange)
- In-line power towers like $2^{\wedge{}}3^{\wedge{}}4$
- “Disagreement on operator precedence for 2^3^4” (walkingrandomly.com)
- “How are exponent towers evaluated?” (brilliant.org)
not sponsored, never paid for their service.
Why does this go viral so often?
Because the actual math is easy almost everybody has an opinion on it.


Most people also don’t know that with weak and strong juxtaposition there are two conflicting conventions available, that can be used to interpret the expression. Some just blindly follow “PEMDAS” and forget (or don’t know) that’s not a mathematical rule, but just a mnemonic to help students memorize the order of operations. But those mnemonics cover just the basics. The actual real world is way more complicated and messier than “BODMAS”.
Even people who know about implicit multiplication by juxtaposition dismiss a lot of details. Probably because of confirmation bias and/or because they don’t want to invest so much time into thinking about stupid social media posts.
What makes it even more tricky is, that the actual problem with the ambiguity can’t be explained in a quick comment, so even if a few people already know that this is an ambiguous problem and comment about it, most people just dismiss that, because they “already know” the answer and a two-sentence comment can’t convince them how and why it’s ambiguous. Also, you reading this article, are the exception. Most people who saw the link probably never clicked it. Those who did, probably scrolled to the bottom of the page, saw how long the post is and closed the tab again, because their time is too important (which is fine) to read something they think they already know. Why read something if you have nothing to learn about the topic that’s so simple that you know for a fact that you are right; everybody else is just stupid.
“The Internet is Worse Than Ever – Now What? (by Kurzgesagt)”
What now?
At this point I hope you understand how and why the original problem is ambiguous.
You don’t have to like it, that with weak and strong juxtaposition we have two conflicting conventions, that can fail to give the same answer even for some very simple looking expressions. You can even think that one of those conventions is better than the other, or that one of the two shouldn’t even be a thing. But everything you read and saw until this point should make it very clear, that not everybody shares your opinion and preferences. There is no mathematically true or objectively better choice here. It’s a matter of taste!
My personal opinion
IMHO the most important thing with this “viral math” expressions is to recognize that there is no real consensus if the weak or the strong juxtaposition should be the dominating convention. I somehow like the approach Mathematica (and Wolfram|Alpha) took, to only apply the strong juxtaposition convention between variables but not between numbers. One could argue that there should also be a strong connection between coefficients and variables (like in $r=C/2\pi$) but as said – it’s a matter of taste.
Trying to interpret inputs in a way that might “seem natural” to most people (like Wolfram|Alpha tries to do for example) typically require many sometimes even complicated rules to handle edge cases. They may seem inconsistent when probed (like we did above) especially for beginners and students those rules might be confusing and look inconsistent and would be even harder to teach than just sticking to a single convention. So, it’s fine to stick to “BIDMAS” in school but be aware that that’s not the full story.
Tools like calculators and CAS should try to prevent ambiguous inputs or should give the user immediate feedback, about how the input was interpreted. If it’s technically not possible or trivial to give the user feedback, it would be better to report it as a syntax error and reject calculating it entirely. It would force the user to think about what they want to calculate. For example, in most popular programming languages implicit multiplication is not valid syntax and will be rejected by the compiler or interpreter.
If you ask me, we should just stop engaging with those kinds of ill-defined expressions, that use implicit multiplication right after a division. There is a reason this page doesn’t have a comment section 🤣. If you encounter such discussions in the wild you could just post a link to this page and hope for the best. Alternatively you could also post the “Viral Math Problem Starter Pack” meme from above. The QR code from the meme also leads to this page.


